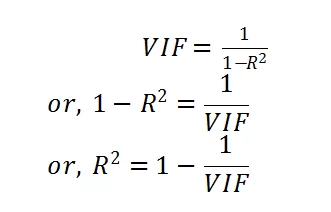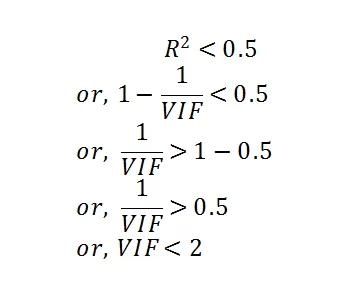Introduction:
Variance Inflation Factor or VIF is basically a measure of multicollinearity of the independent variables in a multiple regression model. Mathematically, the VIF of a regression model is the ratio of the overall model to the variance of a model that includes only that single independent variable. The ratio is calculated for each independent variable. The variable with high Variance Inflation Factor is highly collinear with the other variables in the model.
Why is it important?
While building a model, detecting multicollinearity is a very much important step. We are actually looking for the best model which can explain our dependent variable with the help of the independent variables. Multicollinearity does not reduce the explanatory power of the model. It actually reduces the statistical significance of the independent variables.
What is the threshold of VIF?
There are many theories behind the threshold of VIF. In some books it is written as 10, in some, it is 5 and in some, it is 2. There is no exact measure of the VIF limit. But here we take the threshold of VIF as 2. If the Variance Inflation Factor of an independent variable of the model is greater than 2, it indicates that multicollinearity exists for that independent variable.
Mathematical Interpretation:
Suppose Y is the dependent variable. X1, X2, X3 be the independent variables. The model is,
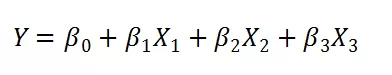
Now, we are interested to check whether multicollinearity exists for the independent variable X1 or not. To check that we need to find the VIF of X1.
We shall now construct the following model to check if the independent variables X2 and X3.
The model is,
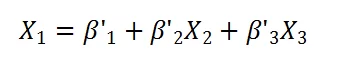
R(Square) be the R-squared value of this model. Then the VIF of X1 is,
So, if X2 and X3 can not explain X1 at least 50% i.e. if R(Square) is less than 0.5 then it can be said that X1 does not depend on X2 and X3. So, there is no multicollinearity of X1 exists.
Now take,
So, if VIF of X1 is less than 2 then the independent variables X2 and X3 can not explain X1 at least 50%. So, X1 does not depend on X2 and X3.
Then it can be said that the multicollinearity of X1 does not exist.
How to remove multicollinearity from the model?
For a model, if we find that multicollinearity exists for one or more independent variables, we simply remove those variables from the model. And further, check the VIFs of the remaining independent variable if there is still multicollinearity or not.
Procedure:
It is not always by trial runs by taking one or combinations of x s having high Variance Inflation Factors and checking under what combination the R-squared adjusted value is highest while all other conditions of regression are satisfied. First we shall take all the independent variables to the multiple regression model. After that the VIF’s of each variable has to be checked. And depending upon the VIF’s the variables with multicollinearity have to be eliminated. As removing multicollinearity does not reduce the explanatory power of the model. So, the R-squared adjusted value will not be affected largely.
Special Case:
In some cases, it can be found that two or more independent variables have VIF greater than 2. And some of the P-values of the independent variables are less than 0.05. In this case, we should eliminate the multicollinearity first. We should not eliminate the independent variables depending upon the P-values at first. In this case, we should eliminate the independent variable with a high VIF value.
Then again run the multiple regression on the remaining independent variables and check the VIF’s. If again there are one or more independent variables that have a VIF of more than 2, then we shall again eliminate the independent variable with a high Variance Inflation Factor value and do the same.
After removing the multicollinearity completely from the model, we shall check the P-values for the significance of the remaining independent variables. Then we may remove the insignificant variables from the model.